singularity

singularity 🔎

• Points
• Vectors
  • Vector Magnitude (aka length aka norm)
• Point and Vector Ops
  • Subtracting Points
  • Adding a Point and Vector
  • Adding Vectors
  • Scalar Product / Multiplying Vector with Number
    • normalize a vector
  • Multiplying Vectors
    • Dot Product
    • Cross Product

Points

Vectors

• Vector ‘represents’ a difference between two Points
• aka an arrow from any point x to any point y
• aka “instructions to get from one point to another”
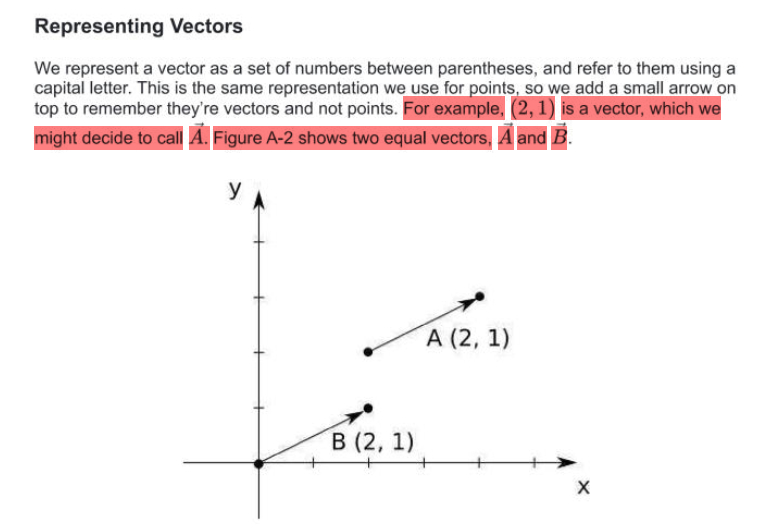
• vectors do not have a position, they are just abstractions over difference between two points
• have a direction = angle in which they point
  • orientation = slope of the line they are on
  • sense = +ve or -ve
• have a magnitude = how long

Vector Magnitude (aka length aka norm)

• m = 1.0 = UNIT VECTOR
• you can compute m from vector coords
• formula: \(|\vec V| = \sqrt{V_{x}^2 + V_{y}^2 + V_{z}^2}\)

Point and Vector Ops

Subtracting Points

• you can subtract two points and get a vector : \(\vec V = P - Q\)
• think of this as “V going from Q to P”
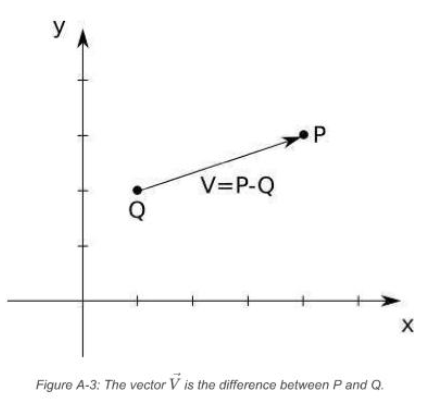
• agebraically, subtract each of the coordinates separately :

\[(V_x,V_y,V_z) = (P_x,P_y,P_z) - (Q_x,Q_y,Q_z) = (P_x-Q_x, P_y-Q_y, P_z-Q_z)\]

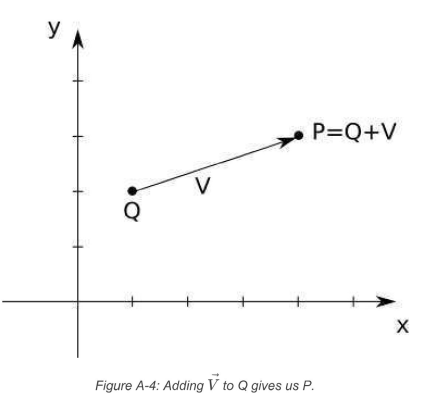
Adding a Point and Vector

\[(V_x,V_y,V_z) = (P_x,P_y,P_z) + (Q_x,Q_y,Q_z) = (P_x+Q_x, P_y+Q_y, P_z+Q_z)\] \[or \\ V_x = P_x - Q_x \\ V_y = P_y - Q_y \\ V_y = P_y - Q_y \\\]

• which means we can do this

\[\\Q_x = P_x + V_x \\ Q_y = P_y + V_y \\ Q_y = P_y + V_y \\ \ \\ thus \\ Q + \vec V = P\]

• you can add a vector and a point to get a new point
• given a starting position (point) and a displacement (vector), you will get a new position / point

Adding Vectors

• imagine putting one vector after another
• commutative = order does not matter
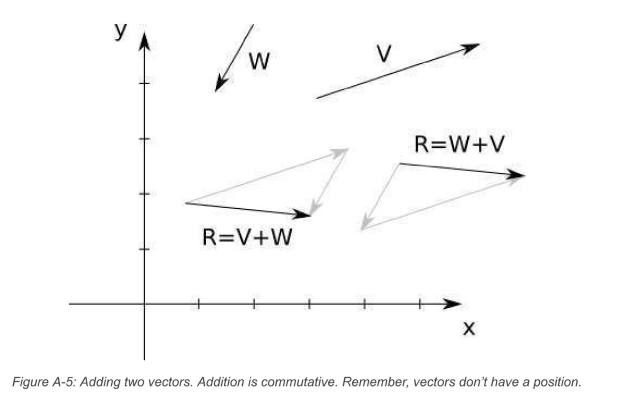
• formally:
• \[\vec V + \vec W = (V_x,V_y,V_z) + (W_x,W_y,W_z) = (V_x+W_x, V_y+W_y, V_z+W_z)\]

Scalar Product / Multiplying Vector with Number

• makes the vector shorter or longer
• if a number is -ve vector will point the other way
• it will remain along the same line
• formally :
• \[k. \vec V = k. (V_x, V_y, V_z) = (k.V_x, k.V_y,k.V_z)\]
• division can be done, except with 0

normalize a vector

• turn it into a vector
• changes the magnitude to 1.0
• to do this divide the vector by its length
• \[\vec V_{normalized} = \frac{\vec V}{|\vec V|}\]

Multiplying Vectors

Dot Product

• \[\langle \vec P \cdot \vec Q \rangle = \langle (P_x,P_y,P_z) , (Q_x,Q_y,Q_z) \rangle = P_x \cdot Q_x + P_y \cdot Q_y + P_z\cdot Q_z\]

• Geometrically, the dot product of V and W is related to their lengths, and to the angle α between them. The exact formula neatly ties together linear algebra and trigonometry:

• \[\langle \vec P \cdot \vec Q \rangle = |\vec P| \cdot |\vec Q| \cdot cos(\alpha)\]
• distributive

• commutative wrt scalar product

• the second formula can be used to calculate the angle between two vectors
• \[\alpha = cos^-1 \left( \frac {\langle \vec P , \vec Q \rangle}{|\vec P| \cdot |\vec Q|} \right)\]

• the dot product of a vector with itself = square of its length

• \[\langle \vec P \cdot \vec P \rangle = P_x^2+P_y^2+P_z^2 = |\vec P|^2\]

• thus, the length of the vector can be calculated thus

• \[|\vec P| = \sqrt{\langle \vec P \cdot \vec P \rangle}\]

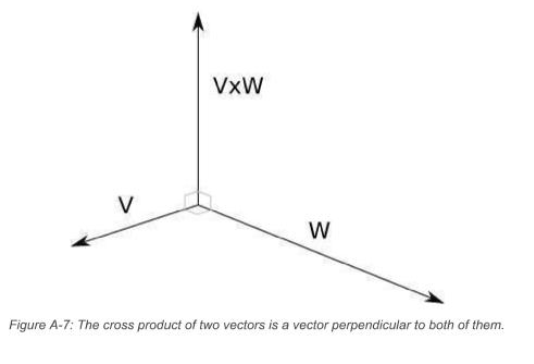
Cross Product

• between two vectors
• gives another vector
• \[\vec V \times \vec W\]
• cross product of two vectors is perpendicular to both of them

• 

• the computation is a bit more involved:
• \[\vec S = \vec U \times \vec R \\ S_x = U_y \cdot R_z - U_z \cdot R_y \\ S_y = U_x \cdot R_z - U_z \cdot R_x \\ S_z = U_x \cdot R_y - U_y \cdot R_x \\\]
• not commutative, specifically:
  • \[\vec U \times \vec R = -(\vec R \times \vec U)\]
• We use the cross product to compute the normal vectored a surface—that is, a unit vector perpendicular to the surface. To do this, we take two vectors on the surface, calculate their cross product, and normalize the result.